Fraction Pie Circle, 360 degrees, with Lesson Ideas for Distance Learning

PRODUCT DESCRIPTION: Fraction Pie Circle, 360 degrees, with Lesson Ideas for Distance Learning by Eve Sutton

TeachersPayTeachers.com > Reachable Teachable store

Fraction-Pie-Circle can be used alone or with ONE-DAY MATH audio tracks 4f and 4g, and Lesson Cards: LC 13 on fractions, decimals, and percents and LC 14: Brick Wall

For the full ONE-DAY MATH course, see: https://reachable.teachable.com

Intuitive, versatile visual for any level of teaching, tutoring, distance learning or home instruction.

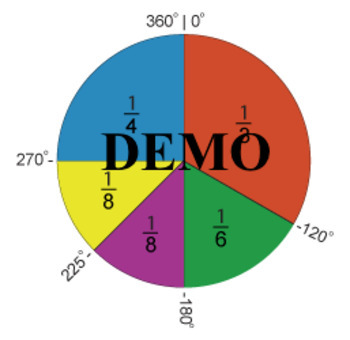
This circle shows both the fractional parts (half, third, fourth, sixth, eighths) and degrees around the circle. Great for hands-on learning with real objects, mental math, and calculations. Instructional levels: PreK, K-8, remedial high school, and Adult Career Skills. Inclusive education: Good visual for dyslexic students. Colors are balanced to work even with red-green color-blind students: the red is more brown, to reduce confusion. Use for general math, geometry, and geography (degrees around Earth).

Suggest printing with COLOR ink on WHITE paper or index/cover stock. Print two copies, and cut one into wedges.

LESSON IDEAS for all instructional levels-- Please copy or print this list. Choose activities that are appropriate for your lessons, and use these ideas to create additional activities in your lessons.

What do you see? The horizontal line between the top number (numerator) and bottom number (denominator) shows a fraction, and a fraction shows a division problem: 1 divided by 2, or 1 divided by 8, etc. After "half" and "third", fraction names end with "th" sound: one-fourth, [one-fifth] one-sixth, [one-seventh], one-eighth.

Here's another way to divide a circle: We divide a circle into 360 degrees going all around, then we come back to zero. You can see this in geometry exercises, and on a globe. The lines meet at the center to form angles. We measure an angle by the number of degrees in that arc of the circle.

FRACTIONS: __Which wedge/section/fraction is larger than the purple section? __Which wedge/section/fraction is smaller than another one, but also larger than another one? __Name them in order, large to small or small to large. __Which two are equal? __Make an addition or subtraction problem showing that two (or three) parts can be equal to another part. Example: 1/8 + 1/8 = 2/8 = 1/4 __Each numerator (top number) = 1, but the denominator (bottom number) changes. __Which is smaller: A fraction with a denominator of 2, or a fraction with a denominator of 3? __A fraction with a numerator of 1 is called a "unit fraction" __In law, mining, or medicine, an "aliquot part" is a portion of a whole amount (of land, or inheritance, or sample to be tested in a lab) that can be represented as a unit fraction. For example, 2/6 = 1/3, so 2 shares (out of 6 equal shares) is an aliquot part.

PROBABILITY, RATIOS: Suppose this circle is a game spinner with an arrow or pointer fastened to the center. Suppose you spin 10 times, or 100 times. __On average, which wedge/color/section will you get most often? Which wedge/color/section is least likely to be chosen? __What two (three, four) areas can be combined to equal another area?

GAMES: Suppose you pay $1 every time you take a turn to spin the arrow, and you start with $10. Which rule is more likely to help you get rich, or lose all your money? __Game A: You get $10 if you land on purple [1 chance out of every 8 spins], but you get nothing if you land on any other color. Game B: You get $2 if you land on red/brown [1 chance out of every 3 spins], but you get nothing if you land on any other color. Game C: You get $2 if you land on blue, yellow, or purple [1 chance out of every 2 spins], but you pay an extra $1 if you land on green.

BASIC OPERATIONS AND ALGEBRA __Compare to an analog clock. What is "half an hour" (quarter of an hour, third of an hour) if the full circle of a clock is 60 minutes? HINT: "of" means "multiply" so think: 1/2 x 60 = 60 divided by 2 = 30 minutes.

__270 – 225 = 45 so 1/8 of the circle is an angle of 45 degrees

__5/8 of 360 = 225

__6/8 (or 3/4, or 75%, or 0.75) x 360 = 225 + 45

__If x = the angle of 1/8 circle, what is 2x? What is 4x?

__If y = angle (degrees) of half a circle, what is 2/3y + 1/3y?

ANGLES and DEGREES: __How many degrees are in a full circle? __How many degrees are in one-half of a circle? (third, quarter, sixth, eighth) __HINT: "of" means "multiply" so think: 1/2 x 360 = 360 divided by 2 = 180 degrees. __Which angles are acute? (smaller than 90 degrees) __Where is a right angle? __HINT: the corner of a sheet of paper is a right angle, 90 degrees. __Which angles are obtuse (wider than 90 degrees)? __When you stand in line and do an "about face" (half a turn), how many degrees are you turning? __Which angles are "complementary" (sum is 90 degrees)? __Which angles are "supplementary" (sum is 180 degrees)? __How many circles (full turns or fractions of a full turn) are described when a snowboarder or skateboarder does a 720 or a 900 or a 1080 degree turn?

__Some polygons have angles of 60 degrees (equilateral triangle), 90 degrees (right triangle, square, rectangle), 120 degrees (hexagon). __The side of any polygon = 180 degrees, a "straight angle" meaning a straight line. __Which pattern blocks match an angle on this circle? __One brown rhombus (diamond) pattern block has a narrow angle of 30 degrees. How many of these narrow angles can fit into the angle of the green wedge? __Use the fraction pie with a protractor to study angles and degrees from both sides (acute vs obtuse angles). __Compare the fraction pie's angles to the angles on pattern blocks.

__Compare the fraction pie's angles to shapes constructed with a compass and ruler.

COMMON CORE STANDARDS, K-8 and High School Geometry:

• CCSS.K.G.B.4
• CCSS.K.G.B.6
• CCSS.K.MD.A.2
• CCSS.K.OA.A.3
• CCSS.1.G.A.3
• CCSS.1.OA.A.2
• CCSS.2.G.A.1
• CCSS.2.G.A.3
• CCSS.3.G.A.2
• CCSS.3.MD.A.1
• CCSS.4.G.A.1
• CCSS.4.G.A.2
• CCSS.4.G.A.3
• CCSS.5.MD.B.2
• CCSS.5.NF.A.2
• CCSS.5.NF.B.3
• CCSS.5.NF.B.4
• CCSS.5.NF.B.6
• CCSS.5.NF.B.7
• CCSS.5.NF.B.7c
• CCSS.6.EE.A.2
• CCSS.6.EE.A.2a
• CCSS.6.EE.B.6
• CCSS.6.EE.B.8
• CCSS.7.G.B.5
• CCSS.8.G.A.1b
• CCSS.8.G.A.5
• CCSS.HSG-C.A.2
• CCSS.HSG-C.A.3
• CCSS.HSG-C.B.5