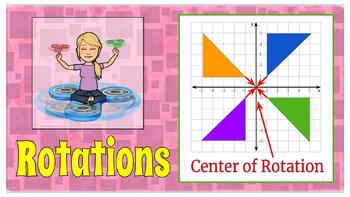
How to Rotate Figures in the Coordinate Plane about the Origin

Also included in
- You are purchasing 7 editable sets of the animated Google Slides used to make these videos. All slides are animated as seen in the video lessons. You may use these slides as guided lessons, scaffolded class notes, print or share student practice slides as task cards, and/or adapt using Pear Deck forPrice $18.40Original Price $23.00Save $4.60
Description
You are purchasing an editable set of the Google Slides used to make this video. All slides are animated as seen in the video lesson. You may use these slides as a guided lesson, scaffolded class notes, print or share student practice slides as task cards, and/or adapt using Pear Deck for whole class instruction.
In this video lesson we will learn how to rotate figures in the coordinate plane about the origin. We will understand that all rotations result an image that is congruent to the original figure. The origin will be the center of rotation. We will rotate using angle of rotations of 90 degrees, 180 degrees, and 270 degrees. We will rotate clockwise and counterclockwise. We will label the image vertices with ' or prime. Student practice is embedded in the lesson with modeled exemplar solutions.